[Home | Kryptographie]

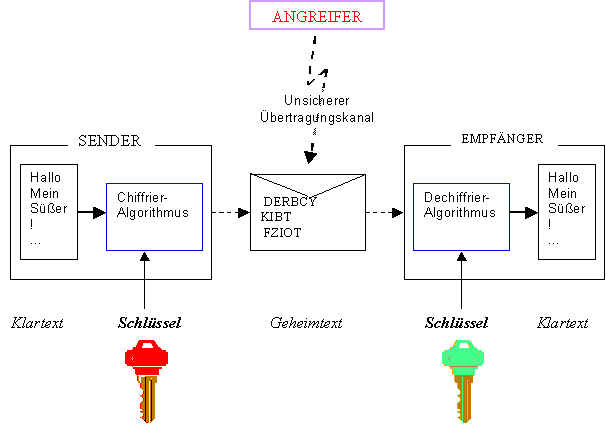
Nachrichtenübermittlung

Der Sender verschlüsselt mit dem öffentlichen Schlüssel des Empfänger, der jedermann bekannt sein kann. Der Empfänger entschlüsselt mit seinem geheimen privaten Schlüssel.

Während bei symmetrischen Verfahren nur einer oder zwei den Schlüssel kennen dürfen, wird dieses Prinzip hier völlig auf den Kopf gestellt: Jeder kennt oder hat den Schlüssel, aber nur einer kann mit dem dazugehörigen privaten Schlüssel lesen.

Der Erfolg hat viele Väter

Dieffie/Hellman-Schlüsseltausch

Alle symmetrischen Systeme litten unter den praktischen Problemen des Schlüsseltauschs. 1976 postulierten sie etwas scheinbar Unmögliches, nämlich dass Verschlüsselung auch ohne einen Schlüsseltausch funktionieren würde, wenn  es etwas gäbe, was in der einen Richtung leicht zu tun sei und in der entgegengesetzten nur sehr schwer. In der Mathematikersprache eine Trapdoor Funktion oder Einwegfunktion, wie z. B. das Suchen einer Telefonnummer nach dem Namen im Berliner Telefonbuch - wer es andersherum versucht, wird bald entnervt aufgeben. Leider fanden sie die Lösung nicht selbst, obwohl es sie schon lange gab - sie musste nur wiederentdeckt werden.

Rivest/Shamir/Adleman

Im Gegensatz zu historischen Verschlüsselungsverfahren wird in der modernen Kryptologie nur noch gerechnet, d. h. Zeichen in Zahlen umgewandelt und damit weitergerechnet. Das berühmte RSA-Verfahren geht auf einen (bereits umgeformten) Satz Eulers aus der Zahlentheorie zurück:

was etwa soviel heißt, wie wenn man eine beliebige Zahl m mit s(p-1) (q-1) + 1 potenziert, dann durch n dividiert, erhält man als Rest wieder die Zahl m. Man braucht "nur" noch diesen Ausdruck in eine Ver- und Entschlüsselungsfunktion aufzuteilen. Wenn man dann noch p und q als Primzahlen wählt und n sehr groß werden lässt, hat man auch die Trapdoor gefunden. Das Multiplizieren von Primzahlen ist sehr leicht, rückwärts ohne Kenntnis ist die Bestimmung der Primzahlfaktoren (Faktorisierung) extrem schwierig und aufwendig. Klar ausgedrückt bedeutet dieses, wer n schnell faktorisieren kann, ist in der Lage RSA zu brechen - anders gesagt, RSA ist nur so sicher wie die (momentane?) Unfähigkeit, große Zahlen in vernünftiger Zeit zu faktorisieren.

Der daraus abgeleitet Verschlüsselungsalgorithmus sieht dann geradezu lächerlich einfach aus:

Beide Partner müssen n haben;
der Absender benutzt e und n, die als öffentlicher Schlüssel bekannt gegeben oder bei einer Stelle hinterlegt werden
Der Empfänger entschlüsselt mit seinem privaten und geheimen Schlüssel d. Da das Verfahren bei hinreichend großen Zahlen als sicher gilt, ist auch das Problem des unsicheren Übertragungskanals für den Schlüssel erledigt.

Nun muss noch geklärt werden, wie man zu diesen Zahlen kommt. Dazu ein RSA Beispiel.